神经网络学习笔记（3） – 梯度下降法

在训练阶段，为了计算网络中和的值，需要把它转化为一个数学上的优化问题。深度神经网络采用的是梯度下降法。
为了便于理解，一个最简单的例子是求解线性回归问题：给定一组二维平面上的点，拟合一条最能描述这些点之间关系的直线。由于我们知道二维平面上直线的表达式是，记估计值。因此问题在于找到和，使得为最小。这个用来衡量估计值和实际值的偏差，并有待最小化的式子就叫做Cost Function。在不同的问题中，可使用不同的Cost Function。
因为我们训练变量和，因此只需构造含有一个神经元的神经网络。将激活函数定义为“输入即输出”，因为并不需要非线性的学习能力。

神奇的梯度下降算法用于在不断的迭代中寻找使Cost Function取最小值时的变量和。在执行该算法时，需先指定一组和的起始值。然后，计算出一个估计值以及。这一步称为正向传播。随后再根据迭代公式进行反向传播，计算下轮的和。
梯度计算公式：

推广到n个神经元：

假设t为迭代的次数，则迭代公式如下：

……
每个待训练的参数要分别进行这个公式的计算。
以为例，它是一个变量为的函数，也即梯度在上的一个分量。简单来说，梯度反映了每个变量的变化对整个结果的变化的贡献。
learning_rate是学习的速率，控制了学习的步长。当其取值太小时，会导致求解速度变缓，而过大则有可能总是错过最优解。因此是一个Hyper Parameter。

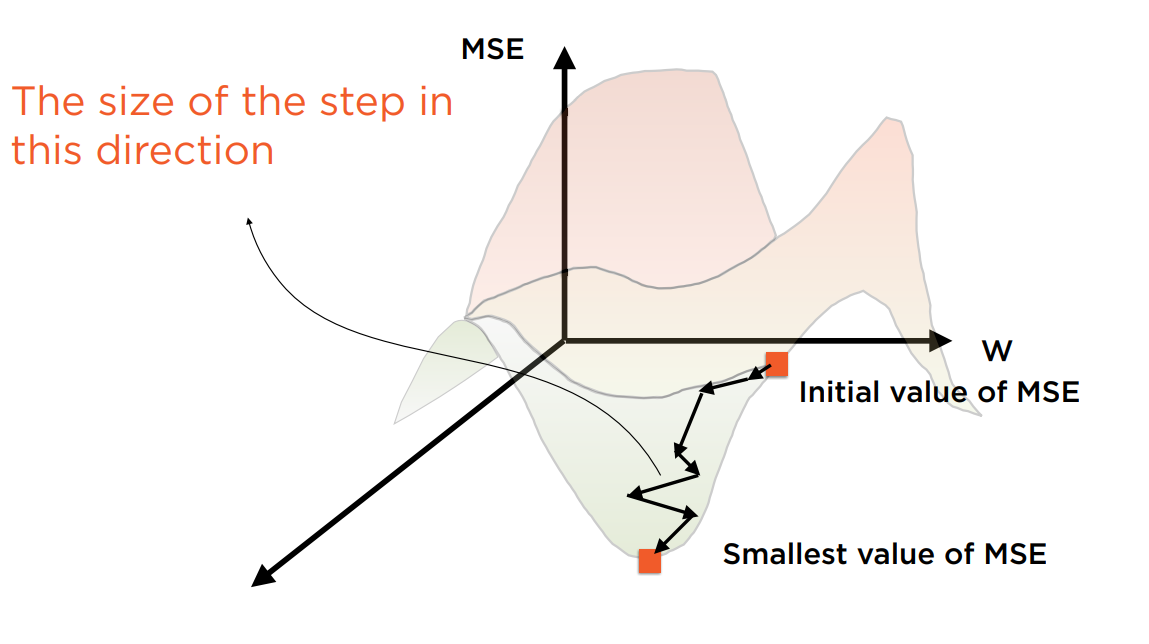
在下一轮迭代中，会变得更小，理想情况下，当的值为0时，就找到了能使最小时的取值。

PyTorch已具有自动计算梯度的功能。通过设置requires_grad，来启用对Tensor计算时梯度的追踪。

以下是对自动梯度计算的尝试。

import torch
tensor1 = torch.Tensor([[1, 2, 3],
[4, 5, 6]])
tensor2 = torch.Tensor([[7, 8, 9],
[10, 11, 12]])
#默认为False
print(tensor1.requires_grad)
#调用该函数启用梯度追踪
tensor1.requires_grad_()
output_tensor = tensor1 * tensor2
#requires_grad具有传播性，为True
print(output_tensor.requires_grad)
#此时计算结果已有一个梯度函数。（梯度函数在输出变量上。）
print(output_tensor.grad_fn)
#反向传播
output_tensor.backward()
#此时能看到tensor1的梯度了。（梯度在输入变量上）
print(tensor1.grad)
#注意到梯度的尺寸和Tensor的尺寸相同。Tensor中每个元素都拥有一个梯度。
print(tensor1.grad.shape, tensor1.shape)
#使用no_grad的block来局部禁止梯度的传播
with torch.no_grad():
    new_tensor = tensor1 * 3
    #新建的Tensor不具有梯度跟踪功能
    print('requires_grad for new_tensor = ', new_tensor.requires_grad)
    #原来的Tensor依旧保留了原来梯度跟踪功能
    print('requires_grad for tensor = ', tensor1.requires_grad)
#也可使用下面的标注来禁止自定义函数的梯度计算功能
@torch.no_grad()
def calculate_with_no_grad(t):
    return t * 2
result_tensor_no_grad = calculate_with_no_grad(tensor1)
#为False
print(result_tensor_no_grad.requires_grad)
#生成不带梯度功能的Tensor副本
detached_tensor = tensor_one.detach()
#为False
print(detached_tensor.grad)

构建单个神经元的神经网络进行线性拟合。为了简化问题，待被拟合的直线被假定通过原点，故只有需要训练。而为了与神经网络同构，使用了w1和w2两个连接上的权值。实际上只需一个变量即可。

x_train = np.array ([[4.7], [2.4], [7.5], [7.1], [4.3], [7.816],
[8.9], [5.2], [8.59], [2.1], [8] ,
[10], [4.5], [6], [4]],
dtype = np.float32)
y_train = np.array ([[2.6], [1.6], [3.09], [2.4], [2.4], [3.357],
[2.6], [1.96], [3.53], [1.76], [3.2] ,
[3.5], [1.6], [2.5], [2.2]],
dtype = np.float32)
X_train = torch.from_numpy(x_train)
Y_train = torch.from_numpy(y_train)
#一个输入值，经过单个神经元的隐藏层，以及一个输出值
input_size = 1
hidden_size = 1
output_size = 1
#使用随机值初始化神经元的输入连接和输出连接的权值。requires_grad设为True开启梯度追踪模式。
w1 = torch.rand(input_size,
hidden_size,
requires_grad=True)
w2 = torch.rand(hidden_size,
output_size,
requires_grad=True)
#设置学习速率
learning_rate = 1e-6
#迭代1000次进行训练
for iter in range(1, 1000):
    #第一步：正向传播。由于激活函数没有启用，估计值就是输入的样本和w1的乘积，再乘以w2
    y_pred = X_train.mm(w1).mm(w2)
    #第二步：计算Loss Function的值（就是Cost function）
    loss = (y_pred - Y_train).pow(2).sum()
    #每50次迭代打印Loss Function的值
    if iter % 50 ==0:
        print(iter, loss.item())
    #第三步：反向传播
    loss.backward()
    #第四步：更新神经元连接的权重值。此时要关闭梯度跟踪。更新完后要清除权重的梯度，以便下次重新计算。
    with torch.no_grad():
        w1 -= learning_rate * w1.grad
        w2 -= learning_rate * w2.grad
        w1.grad.zero_()
        w2.grad.zero_()

#使用训练样本进行预测
x_train_tensor = torch.from_numpy(x_train)
predicted_in_tensor = x_train_tensor.mm(w1).mm(w2)
predicted = predicted_in_tensor.detach().numpy()