神经网络学习笔记（9）- 卷积神经网络结构

由于一张图片的每个像素都是图片的一个特征，若按照最简单的结构，每一层的结点代表一个像素，再进行全连接，就会发生参数爆炸的现象。设想一个100×100的图像，共有10000个像素。每层就有10000个神经元。两层之间的全连接个数就是10000×10000。也就意味着有1亿个参数要训练！
另一方面，视觉在接收信息时，也是以2维团状来感知的。不会一个接一个像素地去看。其中有相当的冗余信息。


CNN中引入了两种为了适合图像信息处理的层：Convolution层和Pooling层。

Convolution层

将一个滑动窗口函数（Sliding window function）作用于一个矩阵上。它是一个像素矩阵。这个函数在卷积计算中称为Kernel或者Filter。
下图是一张灰度图，图上显示的是一个手写数字4。它的像素表示如下：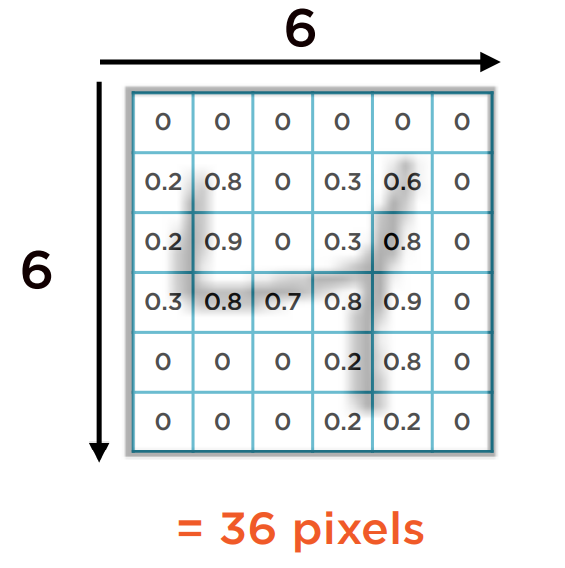

假设使用的Kernel如下：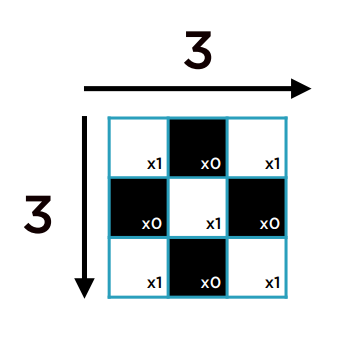

先把Kernel对齐置于矩阵的左上方，进行矩阵的点积运算。点积运算即为每个位置相同的元素的乘积的总和，为一个数。这里大多数格子都为0，只有0.81+0.21=1。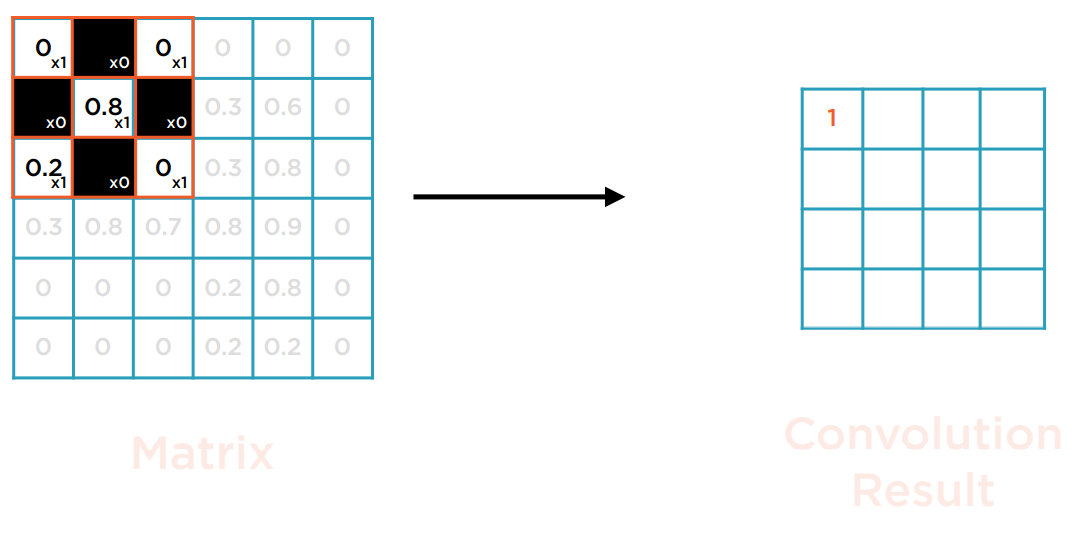

将Kernel从左往右，从上往下，以单个像素为步长滑动，持续进行点积运算。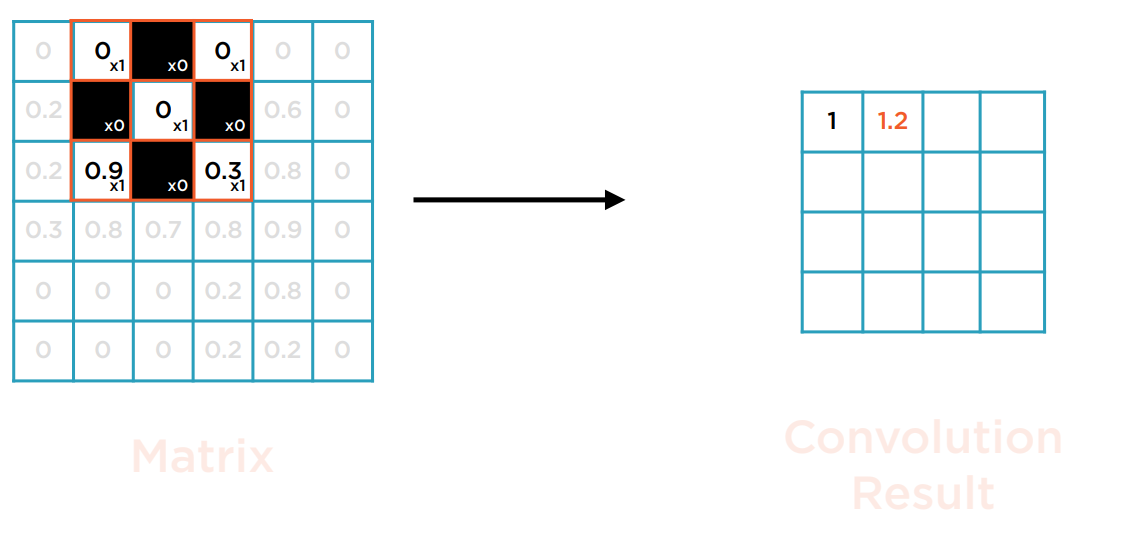

最后，就生成了一个4×4的矩阵。这个生成的矩阵作为像素的表示，也能被视为一张图。这张图叫做Feature map。Feature map的每个元素是卷基层的一个神经元。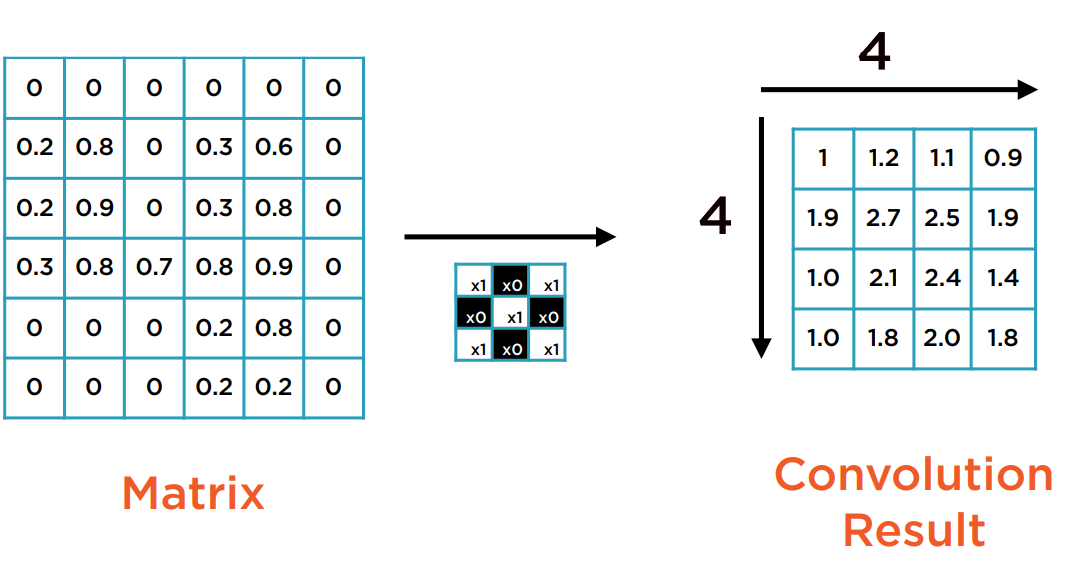

这里还有一些变形：

首先，Kernel一般都使用正方形。Kernel的大小越小，计算量就越小，对性能越友好。
第二，可改变滑动窗口的步长（Stride）。所谓步长就是滑动一次经过的像素数。
第三，当原图的边缘也比较重要时，可以对原图边缘用空白补充一圈，即Zero padding。

注意到，在CNN中，神经网络不再是全连接，且变得非常稀疏。Feature map中的每个神经元与前一层的连接的权值（Weight）和偏移（Bias）都是一样的，因为都是通过与同一个Kernel点积的结果。这使得CNN中待训练的参数大大减少。

而并行地经过一组不同的Kernel后，就能得到一组Feature maps。这组Feature maps就构成了一个卷基层。
如何计算经过CNN层后的尺寸变化（假定图像是正方形）
O = (W-K+2P)/S + 1

其中:

O: 新图边长
W: 原图边长
K: Kernel的边长
P: Zero padding
S: Stride size

Pooling层

在Feature map矩阵上，再执行一个固定大小的滑动窗口函数，仅计算被框住的子矩阵中的聚合函数（如最大值、平均值、求和等）作为输出。如下图所示：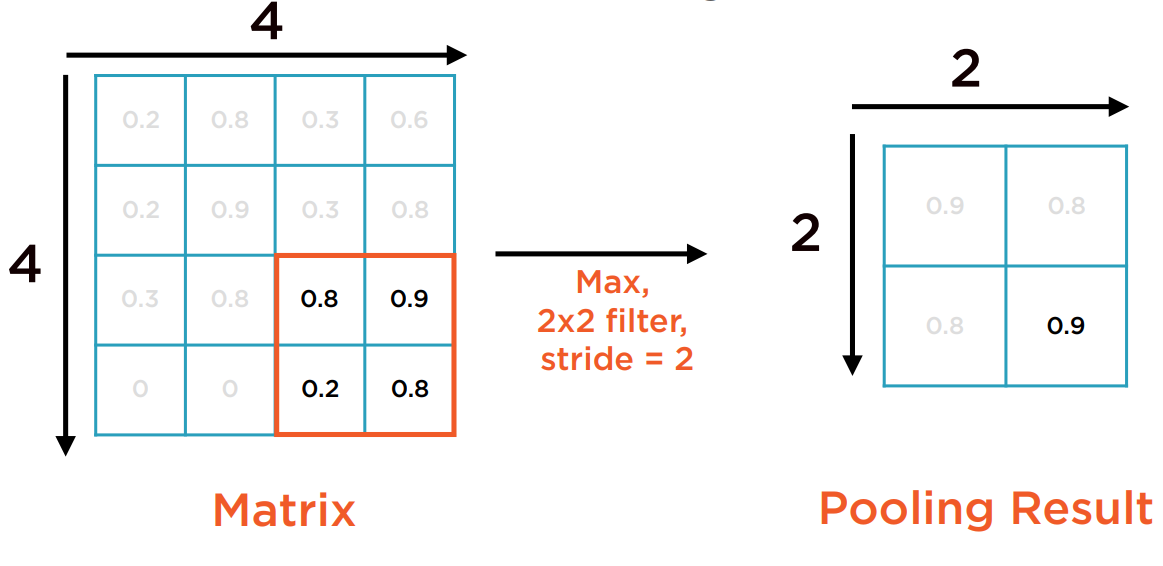

注意到Pooling层没有任何权值（Weight）和偏移（Bias）。无待训练的参数。

Pooling层再次减少了数据规模，且有助于缓解过拟合。

下面展示了一个读取图像并经过卷积层和Pooling层的例子。关注点在于尺寸的变化。

import numpy as np
from PIL import Image
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import transforms as tf

img = Image.open("datasets/images/street.jpg").convert('RGB')

transforms = tf.Compose([tf.Resize(400), 
                        tf.ToTensor()])
img_tensor = transforms(img)
img_tensor.shape #torch.Size([3, 400, 599])                        

#各种预定义的kernal，来自图形学的理论
sharpen_kernel = [[[[0, -1, 0]], 
                   [[-1, 5, -1]], 
                   [[0, -1, 0]]]]
horizontal_line_kernel = [[[[1, 0, -1]],
                           [[0, 0, 0]],
                           [[-1, 0, 1]]]]
vertical_line_kernel = [[[[0, 1, 0]],
                         [[1, -4, 1]],
                         [[0, 1, 0]]]]                           
edge_detection_kernel = [[[[-1, -1, -1]],
                          [[-1, 8, -1]],
                          [[-1, -1, -1]]]]
conv_filter = torch.Tensor(sharpen_kernel) 
conv_filter.shape #torch.Size([1, 3, 1, 3])，对应于batch，颜色通道，高，宽
img_tensor = img_tensor.unsqueeze(0) #torch.Size([1, 3, 400, 599])
conv_tensor = F.conv2d(img_tensor, conv_filter, padding=0) #Feature map尺寸为torch.Size([1, 1, 400, 597])
pool = nn.MaxPool2d(2, 2)
pool_tensor = pool(conv_tensor) #经过2x2的Pooling层后，尺寸为torch.Size([1, 1, 200, 298])

整个CNN的架构如下图所示：

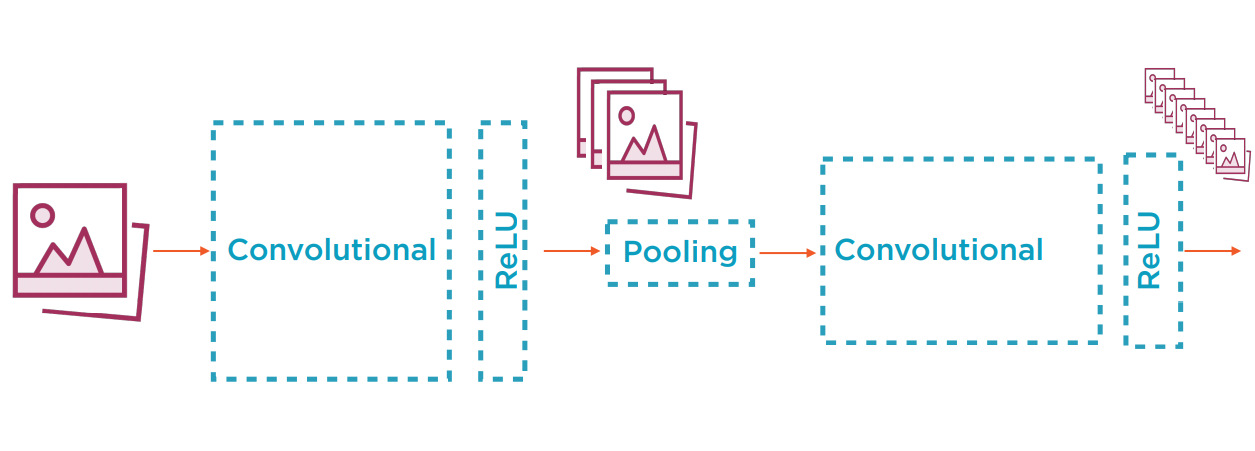
每张图片作为输入，先经过一组卷积层，生成了若干尺寸略小的Feature maps（若有Zero padding则尺寸相同）。通常再通过一个非线性的ReLU层，然后经过Pooling层尺寸减半。如此往复，随着层数越深，生成的Feature map就越多且越小。在最后，接传统的全连接神经网络作为输出。

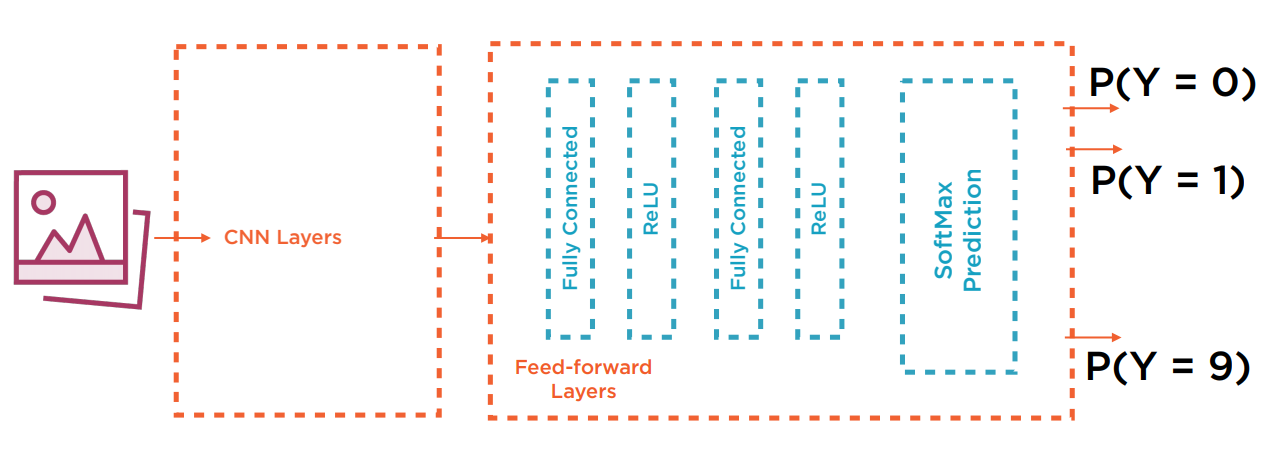
上图作为一个图像分类问题，最后使用了SoftMax输出各个类别的概率预测值。

最后，展示一个使用CNN来进行mnist数据集分类的问题。mnist是一系列手写的0～9的数字的灰度图像，尺寸为28×28。目的是把图片归类为所描绘的数字本身。

采用的CNN网络结构如下
Conv2d: 2维卷积层。
参数
in_channels (int) – 输入图像的颜色通道数（或Feature map个数）
out_channels (int) – 输出图像的颜色通道数（或Feature map个数）
kernel_size (int or tuple) – 卷积Kernel的尺寸

BatchNorm2d: 基于长宽2维进行标准化。
参数
num_features – 输入图像的颜色通道数

ReLU: 激活函数

Maxpool2d: Pooling层
参数
kernel_size – 卷积Kernel的尺寸

Linear: 线性全连接层
参数
in_features – 前一层的输出神经元总数
out_features – 分类的类别数

import torch.nn as nn
import torch.nn.functional as F

in_size = 1 #input size为颜色通道数，1表示灰度图

hid1_size = 16 #第1层生成Feature map的个数（深度）
hid2_size = 32 #第2层生成Feature map的个数（深度）。越是后面的层越深，而图像的尺寸越小。

out_size = 10 #output size为类别数

k_conv_size = 5 #kernel size

class ConvNet(nn.Module):
    
    def __init__(self):
        super(ConvNet, self).__init__()
        
        self.layer1 = nn.Sequential(
            nn.Conv2d(in_size, hid1_size, k_conv_size), #根据公式O = (W-K+2P)/S + 1，默认Stride size为1， zero padding为0，输出的图像边长为24
            nn.BatchNorm2d(hid1_size),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2))    #输出图像边长为12
        
        self.layer2 = nn.Sequential(
            nn.Conv2d(hid1_size, hid2_size, k_conv_size), #输出图像边长为8
            nn.BatchNorm2d(hid2_size),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2))    #输出图像边长为4
        
        self.fc = nn.Linear(512, out_size)  #将32个生成的Feature map所有像素展开成一维：共计4×4×32=512个神经元
        
 
    def forward(self, x):
        out = self.layer1(x)      
        out = self.layer2(out)
        out = out.reshape(out.size(0), -1) #重组成1维
        out = self.fc(out)
        return out


model = ConvNet()

#将计算交给GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)

X_train_tensor = X_train_tensor.to(device)
x_test_tensor  = x_test_tensor.to(device) 

Y_train_tensor = Y_train_tensor.to(device)
y_test_tensor  = y_test_tensor.to(device)

learning_rate = 0.01 

criterion = nn.CrossEntropyLoss()  

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate) 

#Train the Model
num_epochs = 10
loss_values = list()

for epoch in range(1, num_epochs):
        
        outputs = model(X_train_tensor)
        loss = criterion(outputs,Y_train_tensor)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
        print('Epoch - %d, loss - %0.5f '%(epoch, loss.item()))
        loss_values.append(loss.item())

#Evaluate the Model
model.eval()
from sklearn.metrics import accuracy_score, precision_score, recall_score
with torch.no_grad():
    
    correct = 0
    total = 0
    
    outputs = model(x_test_tensor)
    _, predicted = torch.max(outputs.data, 1)
    
    y_test = y_test_tensor.cpu().numpy()
    predicted = predicted.cpu()
    
    print("Accuracy: ", accuracy_score(predicted, y_test))
    print("Precision: ", precision_score(predicted, y_test, average='weighted'))
    print("Recall: ", recall_score(predicted, y_test, average='weighted'))