神经网络学习笔记（7） – 分类问题

对于分类问题，输入的样本或特征维度与线性回归问题没有差异，但输出值不再是一个数，而是一个数组，这个数组的每个元素对应于该样本被归于每个目标类型的概率。当预测时，概率高的那个类别，作为模型预测的结果。

我们知道，在每次事件中，概率模型要求：
1）样本被归于每个类别的概率都为0到1之间的实数
2）归于各个类别的概率总值为1

设想我们已构建了一组神经网络，他有隐藏层，有线性和非线性计算，也可能有Dropout。我们期望的输出的节点数即为类别数，每个节点的值对应于样本被分为该类别的概率。但经过神经网络计算后的值并不符合概率模型要求的2个条件。
为此，需要有一种方法，将任意域的一组数映射到满足这2个条件的空间上。SoftMax函数的作用就是如此。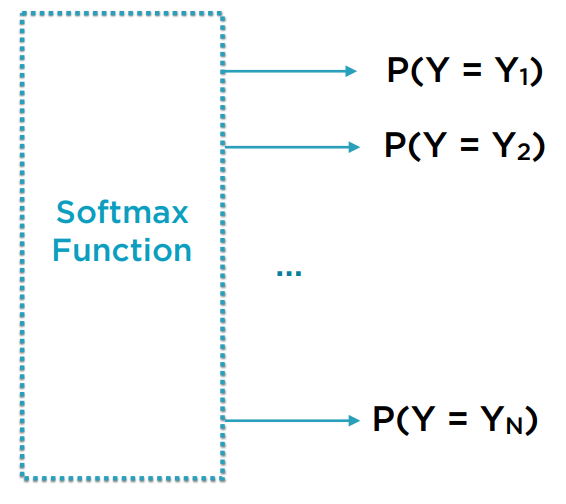


例：
x = [-1.1923, -0.1186, 1.2675]
SoftMax(x) = [0.0640, 0.1872, 0.7488]
不难验证，SoftMax(x)各元素均为0到1之间，且和为1的实数。

Cross Entropy

Cross Entropy用于描述两个概率分布的差异程度。它的数学公式在此不究。它是与SoftMax一起使用的Loss function。

Log SoftMax

将SoftMax取自然对数后ln(SoftMax(x))，就是Log SoftMax。它在数学上和SoftMax等价，但实践下来比起SoftMax更稳定。相应的，要使用NLL(Negative log likelihood)作为它的Loss function。

结果评价

混淆矩阵用于表征各类别的预测和实际结果，具有统计意义。它形式如下图，每一行是实际类别，每一列是预测类别。矩阵中的元素为一次测试落入每种情况的样本总数。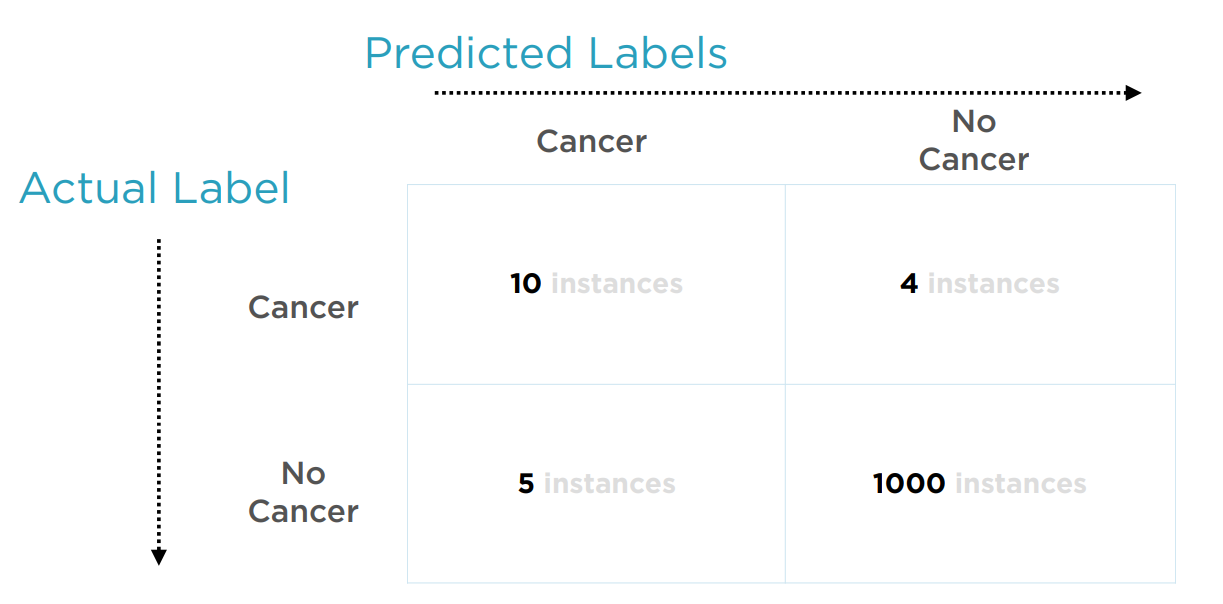

对角线上的值（即预测成功的情况）占总样本数的比例，为Accuracy（准确度）。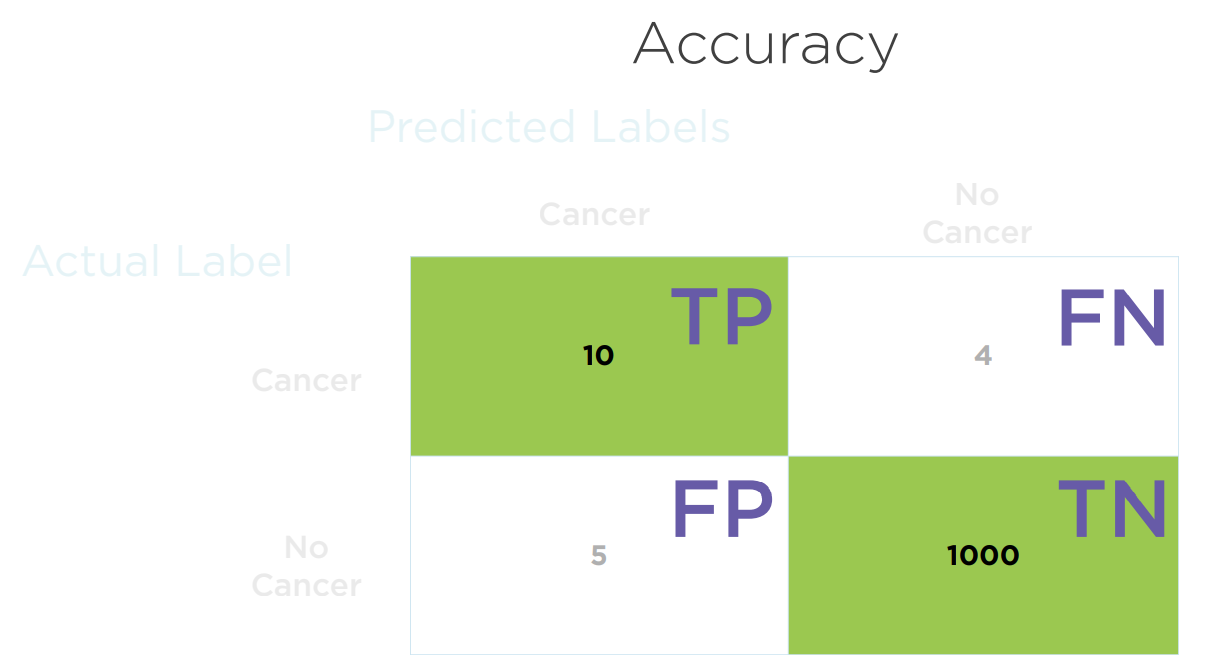

在下面的例子里，使用PyTorch扩展自定义神经网络类，解决分类问题。这里用了2个隐藏层，每个有hidden_size个节点。input_size为特征数，output_size为类别数。forward方法编写了正向传播的逻辑。

import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):

  def __init__(self,hidden_size, activation_fn = 'relu', apply_dropout=False):
    super(Net, self).__init__()

    self.fc1 = nn.Linear(input_size, hidden_size)
    self.fc2 = nn.Linear(hidden_size, hidden_size)
    self.fc3 = nn.Linear(hidden_size, output_size)

    self.hidden_size = hidden_size
    self.activation_fn = activation_fn

    self.dropout = None
    if apply_dropout:
      self.dropout = nn.Dropout(0.2)

  def forward(self, x):

    activation_fn = None
    if self.activation_fn == 'sigmoid':
      activation_fn = F.torch.sigmoid

    elif self.activation_fn == 'tanh':
      activation_fn = F.torch.tanh

    elif self.activation_fn == 'relu':
      activation_fn = F.relu

    x = activation_fn(self.fc1(x))
    x = activation_fn(self.fc2(x))

    if self.dropout != None:
      x = self.dropout(x)

    x = self.fc3(x)
    return F.log_softmax(x, dim = 1)#log_softmax函数的参数dim指定了在哪个维度进行SoftMax计算。根据PyTorch的约定，一般第0维为样本索引，因此在第1维上计算。dim也可为负数，表示倒数第几维。

import torch.optim as optim
def train_and_evaluate_model(model, learn_rate=0.001):
  epoch_data = []
  epochs = 1001

  optimizer = optim.Adam(model.parameters(), lr=learn_rate)

  loss_fn = nn.NLLLoss()#因使用Log SoftMax,必须对应使用NLLLoss作为Loss Function。

  test_accuracy = 0.0
  for epoch in range(1, epochs):

    optimizer.zero_grad()
    #训练集正向传播与反向传播
    Ypred = model(Xtrain)

    loss = loss_fn(Ypred , Ytrain)#此处Ypred的尺寸为[样本数,类别数]，为经log_softmax映射后的数组；Ytrain的尺寸为[样本数,1]，对应于类别的索引值。
    loss.backward()

    optimizer.step()
    #测试集进行评估
    Ypred_test = model(Xtest)
    loss_test = loss_fn(Ypred_test, Ytest)

    _, pred = Ypred_test.data.max(1)#pred获取概率最大的类别的索引

    test_accuracy = pred.eq(Ytest.data).sum().item() / y_test.values.size #准确率为预测正确的样本数占总样本数的比例

    epoch_data.append([epoch, loss.data.item(), loss_test.data.item(), test_accuracy])

    if epoch % 100 == 0:
      print ('epoch - %d (%d%%) train loss - %.2f test loss - %.2f Test accuracy - %.4f'\
         % (epoch, epoch/150 * 10 , loss.data.item(), loss_test.data.item(), test_accuracy))

  return {'model' : model,
    'epoch_data' : epoch_data,
    'num_epochs' : epochs,
    'optimizer' : optimizer,
    'loss_fn' : loss_fn,
    'test_accuracy' : test_accuracy,
    '_, pred' : Ypred_test.data.max(1),
    'actual_test_label' : Ytest,
       }
net = Net(hidden_size=3, activation_fn='sigmoid', apply_dropout=False)
result_3_sigmoid = train_and_evaluate_model(net)
_, pred = result_3_sigmoid['_, pred']
y_pred = pred.detach().numpy()
from sklearn.metrics import confusion_matrix, recall_score, precision_score
confusion_matrix(Ytest, y_pred)#混淆矩阵